But small size is not the only requirement. Consumers will soon demand handsets that can handle all their wireless communication needs—Wi-Fi, Bluetooth, hookups with wireless sensor networks, cellular calls, broadcast television, even satellite links. And to do all that practically, designers will be compelled to put resonators of many different frequencies on a single chip. Unfortunately, the frequency of an FBAR resonator is set by the thickness of its constituent film, which means, for example, that 20 different deposition procedures would be needed to fabricate 20 different filters on the same chip. Doing so would likely end up being more expensive than just buying 20 individual FBAR devices.
Here’s where the latest wizardry of microelectromechanical systems (MEMS) can save the day. A single layer of silicon, for example, can provide many different resonant frequencies if it is patterned so that parts vibrate from side to side, in directions parallel to the plane of the device. The designer just needs to create features with the correct lateral dimensions.
Easier said than done, of course. To get a sense of the challenge, consider a more familiar object whose lateral dimensions govern its resonance frequency: a steel guitar string, which spans about 64 centimeters. If tuned to middle A, it will have a fundamental resonance frequency of 110 hertz. The act of plucking a guitar string is capable of exciting any frequency, but this string will mechanically select just the one A note—and will do so with a Q of about 350. (That, by the way, is 50 times as good as a typical on-chip electrical circuit made of inductors and capacitors.)
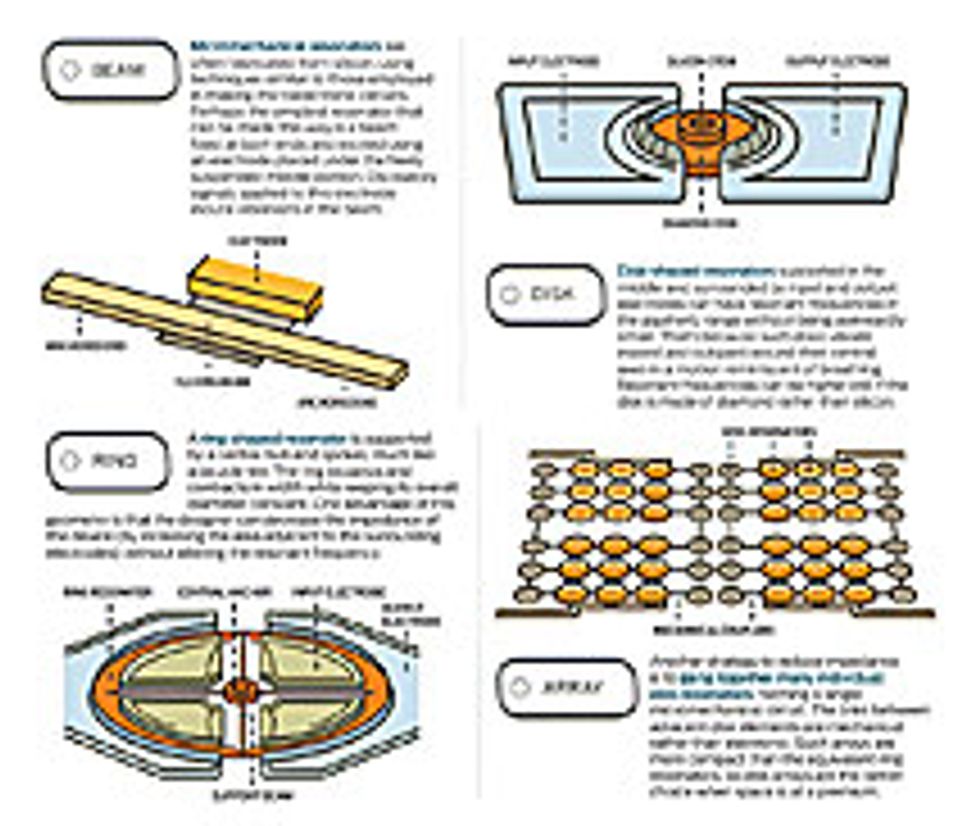
Selecting a particular frequency is exactly what the filters of a radio do. Of course, they oscillate much faster than a guitar string vibrates, commonly hundreds of millions of times a second. To achieve such rates, you’d have to shrink a guitar string down to less than 10 µm and construct it out of a stiffer material, such as silicon. The result would be a tiny, flexible beam. You couldn’t pluck such an object with a pick, of course, but you could easily excite it with an electric field. Such a micromechanical oscillator can be made to resonate with Qs in excess of 10 000.
As you might guess, shrinking things by another factor of 10 yields resonant frequencies in the gigahertz range, which are needed to reach the higher bands used for wireless communications today. However, as with nanometer-size electronics, some thorny engineering issues arise with mechanical resonators this small. For one, it’s hard to control the resonance frequency precisely when the dimensions are so tiny. And even if you could do that consistently, you’d probably find that what you’d built couldn’t handle much power.
Fortunately, there are ways to achieve gigahertz-range resonant frequencies without having to reduce dimensions to nanometer scale. My colleagues and I at the University of California, Berkeley, have, for example, fabricated some very useful gigahertz-frequency MEMS devices that measure several micrometers across. They can be tuned to the desired frequency relatively easily and are large enough to handle the power levels found in receiving circuitry. We’ve made them by fashioning the moving parts in the shape of thin disks, which resonate by expanding and contracting radially ever so slightly, rather than flexing like a beam.
If you make such a disk out of diamond instead of silicon, it will be stiffer and will consequently resonate at frequencies that can easily exceed 1 gigahertz. And if you arrange things so that this disk is supported only at its center—a point that doesn’t move during the in-and-out oscillation—using a slender stem of silicon, the quality factor for this resonator can be stunningly high. We’ve built ones that measure 10 µm across, run at 1.5 GHz, and have Qs of more than 10 000—even higher when the air between the disk and the surrounding electrodes is removed. Versions of such disks running at 500 megahertz give Qs greater than 50 000.
This approach not only achieves the kinds of frequencies you’d want without having to build nanoscale objects, it also eliminates the need to use a vacuum to achieve high Q, reducing manufacturing costs. And because the resonant frequency of such a disk is roughly inversely proportional to its radius, even higher frequencies—such as Wi-Fi’s 2.4-GHz, 3.6-GHz, and 5-GHz bands—with similar Qs should be possible simply by reducing the size.
But there’s a limit to how much you can shrink things before the complications of working at the nanoscale start to emerge. Thankfully, we’ve discovered ways to dodge this problem. And happily enough, they don’t require the use of diamond, which can be expensive to manufacture. In fact, all-silicon resonators can perform just as well, if not better, when constructed with somewhat more complicated geometries.
My colleagues and I have had success, for example, with resonators that take the form of a ring attached to a central support with four spokes. The ring expands and contracts in width while its average diameter remains fixed. (Imagine a bicycle wheel with just its rubber tire expanding and contracting slightly.) Our resonators can vibrate in this way at very high frequencies and, if properly designed, without losing much energy through their ”spokes.”